「進階數學及科學/月考2/莊坤霖」修訂間的差異
跳至導覽
跳至搜尋
| 第54行: | 第54行: | ||
#*<img src='http://jendo.org/SVG/images/abc4.svg' width='300px' height=*/> | #*<img src='http://jendo.org/SVG/images/abc4.svg' width='300px' height=*/> | ||
'''題組四:''' | '''題組四:''' | ||
| − | + | ||
'''題組五:''' | '''題組五:''' | ||
| 第61行: | 第61行: | ||
#(fg)'=f'g+fg' (前導後不導+前不導後導) | #(fg)'=f'g+fg' (前導後不導+前不導後導) | ||
#dy/dx=dy/dz*dz/dx ( 分子分母同乘d(g(x)) ) | #dy/dx=dy/dz*dz/dx ( 分子分母同乘d(g(x)) ) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </table> | ||
| + | </form></div> | ||
| + | <div> | ||
| + | <table style='border:#000 solid 1px;border-collapse:collapse;'> | ||
| + | <tr><th colspan=2 style='border:#000 solid 1px;border-collapse:collapse;'>dot</th><th style='border:#000 solid 1px;border-collapse:collapse;'>1</th><th style='border:#000 solid 1px;border-collapse:collapse;'>2</th><th style='border:#000 solid 1px;border-collapse:collapse;'>3</th><th style='border:#000 solid 1px;border-collapse:collapse;'>4</th><th style='border:#000 solid 1px;border-collapse:collapse;'>5</th><th style='border:#000 solid 1px;border-collapse:collapse;'>6</th><th style='border:#000 solid 1px;border-collapse:collapse;'>7</th><th style='border:#000 solid 1px;border-collapse:collapse;'>8</th><th style='border:#000 solid 1px;border-collapse:collapse;'>9</th><th style='border:#000 solid 1px;border-collapse:collapse;'>10</th><th style='border:#000 solid 1px;border-collapse:collapse;'>11</th></tr> | ||
| + | <tr><th colspan=2 style='border:#000 solid 1px;border-collapse:collapse;'>x</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.1</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.2</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.4</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.5</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.6</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.7</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.8</th><th style='border:#000 solid 1px;border-collapse:collapse;'>0.9</th><th style='border:#000 solid 1px;border-collapse:collapse;'>1</th></tr> | ||
| + | <tr><th rowspan=2 style='border:#000 solid 1px;border-collapse:collapse;'>S</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>y</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.1485</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.294</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.4365</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.576</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.7125</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.846</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0.9765</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.104</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.2285</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.35</th></tr> | ||
| + | <tr><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>slope</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.485</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.455</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.425</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.395</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.365</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.335</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.305</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.275</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.245</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.215</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'></th></tr> | ||
| + | <tr><th rowspan=2 style='border:#000 solid 1px;border-collapse:collapse;'>S'</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>y</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.5</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.47</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.44</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.41</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.38</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.35</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.32</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.29</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.26</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.23</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>1.2</th></tr> | ||
| + | <tr><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>slope</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'></th></tr> | ||
| + | <tr><th rowspan=2 style='border:#000 solid 1px;border-collapse:collapse;'>S''</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>y</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>-0.3</th></tr> | ||
| + | <tr><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>slope</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'>0</th><th style='border:#000 solid 1px;border-collapse:collapse;font-weight:normal;padding:2pt;'></th></tr> | ||
| + | </table> | ||
於 2017年1月12日 (四) 14:31 的修訂
題組一:
- 設時間為 x 軸,位移為 y 軸, y=-0.15*x2+1.5x ,求速度方程式與加速度方程式。
- 畫圖:
- 位移-時間命名為 s(x) 。
- 速度-時間命名為 s'(x) 。
- 加速度-時間命名為 s''(x) 。
- 說明:每圖兩種曲線
- s'是s的切線斜率,取 x 為 0.2,0.4,0.6,0.8,1.0 時 s 在各點趨近的切線斜率,及 s' 在上述各點的值,比對兩者是否相符。(提示:取「切線斜率」時,點要密一點;但取值時點不用很密)
- s''是s'的切線斜率,取 x 為 0.2,0.4,0.6,0.8,1.0 時 s' 在各點趨近的切線斜率,及 s'' 在上述各點的值,比對兩者是否相符。
- 兩點之間的∆s=s'與 x 軸所夾的面積,求 x= 0.2 ~ 0.8 之間s'與 x 軸所夾的面積,及 s 在 0.2 與 0.8 的值,比對 ∆s 是否等於 s'與 x 軸所夾的面積。
- ∆s'=s''與 x 軸所夾的面積,求 x= 0.2 ~ 0.8 之間 s'' 與 x 軸所夾的面積,及 s' 在 0.2 與 0.8 的值,比對 ∆s' 是否等於 s'' 與 x 軸所夾的面積。。
題組二:求微分
- 2x4
- 4x3
- -3x
- 2
- 4√x
- 2x4+4x3-3x+2
題組三:x2-4x-1
- x2-4x-1=0,用配方法求兩根。
- 對 y=x2-4x-1 畫圖,求最大值或最小值、兩根。
- 說明係數與圖形的關係。
題組四: 用鋁片做容量 125cm3之正方柱形罐頭,用什麼尺寸才可使材料最節省。
題組五: 說明求導法則
答案:
題組一:
題組二:求微分
- 8X3
- 12X2
- -3
- 0
- 2*1/√X
- 8X3+12X2-3
題組三:x2-4x-1
- X=2±√5
- -5
- 最大係數>0開口向上,最大係數<0開口向下
題組四:
題組五:
- 常數'=0
- (Cƒ(x))'=Cƒ'(x) (提出常係數)
- (fg)'=f'g+fg' (前導後不導+前不導後導)
- dy/dx=dy/dz*dz/dx ( 分子分母同乘d(g(x)) )
</form>
| dot | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
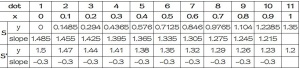
| S | y | 0 | 0.1485 | 0.294 | 0.4365 | 0.576 | 0.7125 | 0.846 | 0.9765 | 1.104 | 1.2285 | 1.35 |
| slope | 1.485 | 1.455 | 1.425 | 1.395 | 1.365 | 1.335 | 1.305 | 1.275 | 1.245 | 1.215 | ||
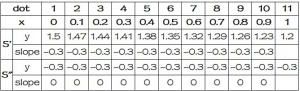
| S' | y | 1.5 | 1.47 | 1.44 | 1.41 | 1.38 | 1.35 | 1.32 | 1.29 | 1.26 | 1.23 | 1.2 |
| slope | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | ||
| S'' | y | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 | -0.3 |
| slope | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||