統計與機率

基本架構

1. 蒐集數據
2. 演算
3. 預測

有一點像算命

用途

• 賭博與賭博設計
• 保險，風險管理
• 投資理財
• 幾乎每一件事(大數據)
  1. 百貨公司

     有一天，百貨公司寄了一份嬰兒用品型錄給你未婚的女兒。你認為這是對你女兒的侮辱，所以怒氣沖沖地打電話到百貨公司客服部抱怨，請他們以後不要再做這種事了。你抱怨完，卻看到女兒興味盎然地翻著型錄，原來她已經懷孕了。

     百貨公司比爸爸更早知道女兒懷孕的消息，不是黑色幽默，而是塔吉特（Target）百貨真實發生的事件。塔吉特怎麼知道顧客懷孕了？說穿了並不神奇，因為該公司設有準媽媽禮物登記處，讓準媽媽們登記自己想要的嬰兒禮物。由於這份清單等於確知已懷孕的顧客名單，塔吉特便依據名單上的消費紀錄，建立起懷孕婦女的購物模式（孕期會購買的商品清單），再用此模型比對其他客人的消費紀錄，找出消費形態類似的顧客，向她們行銷相關商品，達成「未卜先知」的結果。運用這個方法，塔吉特多找出了30%的行銷對象。

  2. 傳染病散布途徑
  3. 解除治理走向「暴政」的兩大根本限制

名詞

• 樣本：蒐集起來觀察，準備用來演算、推論、預測的數據
• 平均數：所有樣本加起來/樣本個數
• 眾數：樣本中出現最多的數
• 中數或中位數：把所有觀察值按高低排序，位在正中間的數
  1. 找本班身高的平均數、眾數、中位數
  2. 找本班BMI的平均數、眾數、中位數
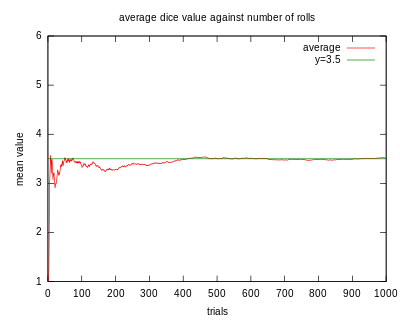
• 大數法則：
  1. 偶然中包含著必然。
  2. 樣本數量越多，則其平均就越趨近期望值。
  3. 對物理量的測量實踐中，測定值的算術平均也具有穩定性。
     

     

     以擲單個骰子的過程來展示大數定律。隨著投擲次數的增加，所有結果的均值趨於3.5(骰子點數的期望值)。在投擲數量較小的時候(左邊)會表現得比較不準，當數量變得很大(右邊)的時候，它們將會很準。
• 期望值：按理應該出現的值，如單顆骰子點數的期望值是1*⅙+2*⅙+3*⅙+4*⅙+5*⅙+6*⅙=3.5
  注意：3.5不屬於 1~6 六種可能結果中的任一個，所以期望值不是期望出現的結果。
• 全距：最大數-最小數
• 標準差：
  1. 算出平均值
  2. 所有(樣本值-平均值)²加起來
  3. 除以樣本個數
  4. 開平方
• 常態分布：

誤用

• 誤把獨立事件當成不獨立事件思考

動畫電影蒐集資料

• 蒐集資料